材料力学の片持はりの問題の解き方を解説します。
私だったらこう解くなーという解き方です。
解き方だけではなく材料力学の問題を解くときの考え方も解説していくので是非参考にしてください。
それでは行きましょう。
問題
以下の図のような片持はりの問題を考えます。
棒の片方が壁面に固定されている状況で先端に荷重Fがかかっている状態です。
この状態で任意の座標xでのせん断力と曲げモーメントを求めようという問題です。

回答
点xでのせん断力と曲げモーメントをそれぞれFx, Mxとすると
Fx=F
Mx=F(L-x)
です。
解き方
先端に荷重Fがかかっていますがもちろんはりは壁面に固定されたままです。
したがって運動量保存則よりはりに働いている力は釣り合っていると考えられます。
つまり以下のようにはりだけを考えるとはりが動かないためにはFと大きさが同じで逆向きの力Wが壁面から働いていなければなりません(運動量保存則)。
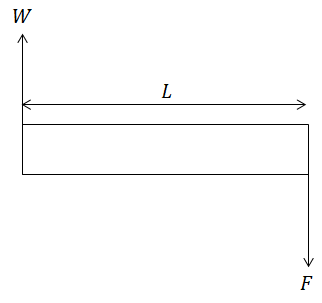
よって
F=W
が成り立ちます。
問題で求めよと言われているのは任意の点xでのせん断力なのでこれをFxとしましょう。
下の図のようにはりを壁からxのところで取り出します。
そうすると根本にはWが働いています。
はりが動かないためにはこのWと釣り合うためにFxが点xのところで働いていなければなりません(運動量保存則)。

つまり
Fx=W=F
です。
これではりのせん断応力Fxは求まりました。
つづいて曲げモーメントを求めましょう。
これはモーメントの釣り合いを考えてあげればいいですね。
ここでもやはりはりだけを考えてあげると以下の図のようになります。
はりにはFによるモーメントF*Lが働いています。
はりが回転しないためにはF*Lと大きさが同じで向きが反対のモーメントMが壁から働いていなければなりません(角運動量保存則)。

よって
M=FL
です。
さて問題で求めろといわれているのは曲げモーメントです。
下の図のように壁から任意の点xではりを取り出すと根本にはMがかかっています。
さらに点xでは先程求めたせん断力Fxがかかっています。

点xでの曲げモーメントをMxとします。
上の図ではりが回転しないためにMはMxおよびFxによるモーメントの和と釣り合わなければなりません(角運動量保存則)。
よって
M=Mx+Fxx
が成り立ちます。
上式にM=FLおよびFx=Fを代入すれば
Mx=F(L-x)
となります。
まとめ
いかがでしょうか。
重要なのは運動量保存則と角運動量保存則を意識して適用できるかどうかですね。
公式を覚えたり、機械的になんとなくで問題を解いているのではちょっと変わった問題が出てきたら解けなくなります。
あとははりを切り出してきたときにすべての力とモーメントを描いてあるかどうかです。
すべての力とモーメントを描いたらあとは運動量保存則と角運動量保存則を適用すればいいだけです。単純ですね。
以上、ありがとうございました。



コメント